I decided that I was not going to die today.
And with that I closed the throttle and, as the nose of my fighter jet lazily dropped below the horizon, I rolled out on a rough heading for home.
‘Jester 3 is bingo, RTB.’ I called over the radio, letting the other two aircraft that I was with know that I was heading home and on minimum fuel.
I was on fumes.
It’s a daily occurrence when you are flying to one of the most tightly packed flying schedules in the world. In order to maximise the training value for the student pilots you have to stay in the air for as long as possible and that often means running your fuel down to frighteningly low levels. Think of it as driving past a fuel stop in the hope of reaching another one even though your car’s fuel light has been on for the last 10 miles.
Except there is no hard-shoulder to park in should you get it wrong.
And the penalties for making mistakes become harsher depending on the discipline being flown. If you are flying a low-level navigation sortie, intending to pull up and fly home some 100-odd miles away from your base airfield, you calculate your required fuel to get home on the ground before you even get airborne. This way you can check that your fuel airborne matches the fuel you calculated in the planning phase when you were on the ground and your head wasn’t trying to do a million other things.
If you are conducting some upper air exercises, again, fuel planning is not too difficult and you can recover home with an excess of fuel, the result of the aircraft burning less fuel at height and with the use of mid-range power settings.
But one of the most demanding scenarios for any pilot comes during ‘air combat manoeuvring’ or ACM. When in combat, a pilot is required to ‘max perform’ his own aircraft and, to do this, they will use any lift augmentation devices that might increase the turn rate whilst simultaneously trying to minimise drag. Lift creates drag and this is called ‘lift-induced’ drag. In order to overcome the drag that is caused by these devices, combat flap, slats or wings etc, a pilot will require as much power from the engine as they can get.
And power requires fuel and lots of it.
In the Tornado GR4, the use of Combat (or max reheat) would use 700 kgs of fuel per minute and the jet only carried 7 tonnes – a pilot can use all of the fuel in just 10 minutes! Combat power is used in air combat and, at the rate it is used, it can catch people out.
And it’s always the hostile aircraft who tends to run out of fuel first when practising air combat – this is because they are permanently engaged in the fight and the throttle is left open for the entire engagement; the other two aircraft just take it in turns to fight the hostile.
I’d like to say that there is a super accurate way in which we calculate our fuel whilst in a fight but, in all honesty, it just takes some rough maths mixed with a healthy dose of experience. It’s why we don’t just allow anybody to be the hostile aircraft in an Air Combat engagement because, when the maths is a little too rough, the experience needs to be incredibly refined.
The maths is rough for a reason, it’s because the aircraft is never actually displaying to us the true amount of fuel we have left. In fact it won’t be accurate until we stop throwing the jet about and allow the fuel to settle – it is only at this point that we truly know how much fuel we have to get home.
And it can be a truly horrible few seconds until the truth finally emerges, like being slowly dealt the last card in a Poker hand – ‘Come on fuel,’ I’ve often caught myself saying ‘that’s not the number I’m needing today!’
We always have a fuel figure that has been calculated on the ground, prior to us getting airborne. Pilots do as much as they can in the planning phases pre-flight as it means that we have less to do airborne when everything seems to be trying to take up our time. We work out how much fuel we need to leave our home airfield with to fly straight to our diversion airfield. We have a diversion should we try and land back home and find that somebody has crashed on the runway preventing us from landing. We then add on an extra fuel considerations we might require such as fuel to conduct an instrument approach versus a visual recovery (an instrument approach being mandatory should we be using a civilian airfield or the weather at our home airfield is poor) and requiring another 80 kgs of fuel. If we have to cross any controlled airspace we will also add some more fuel in case we are delayed and then we add all of this fuel together and arrive at a figure. We call this figure our FOG or ‘fuel on the ground’ and, should we reach this prior to landing, then we either divert to our diversion or declare an emergency and land ahead of all other aircraft at our home airfield.
So, when we fly we have a fuel figure called a ‘bingo’ fuel and to this we can add an element of range or distance back to our intended landing airfield. In the upper air above 10,000 feet we might add twice range to home, at low level we might add more. Either way, the range is dynamic, it is ever changing but our figure that we add it to, our ‘bingo’ figure, should never need to change unless our diversion or weather back home alters which isn’t often.
On a good weather day, when the airfield of Mona, about 10 miles from RAF Valley, is our primary diversion, we will hold about 200 kgs of fuel. This ensures that we can leave Valley, fly to Mona and land before the engine is starved of fuel and stops.
Engines stopping in the air goes against most aviation principals and is generally considered to be a bad thing.
So, let’s talk about the maths pilots use to make sure they bring the aircraft home at the end of the day.
Sometimes the maths is done for range, ie. how far can I fly and other times for endurance – how long can I stay airborne for. And sometimes, when it’s really critical, you’ll end up redoing the maths many times over.
I was once recovering a Tornado GR4 from Cyprus to Sigonella in Southern Italy. The weather was poor and the flight was going to be long, over five hours if I remember correctly. I was in the front four jets and behind us, by about an hour, was the next four. As we approached the Eastern coast of Sicily, one of the back four jets came up on the radio declaring an emergency. He’d shut down an engine with a failure and was now slow, burning more fuel on the one engine than he would be with two (due to flying a lower speed, requiring more lift and hence drag, and requiring a higher power setting) and was requesting an immediate approach into the Sigonella airbase.
In my formation there was a collective sigh of ‘noooooooo!’ as we all knew what this meant!
His ‘May Day’ call meant that nobody was going to be able to land until he did and the Italians were not going to budge. He’d declared an emergency and had priority even though he was still two hours flying time away and we were just 30 minutes. We spent the next hour or so burning as little fuel as we could whilst orbiting in the overhead – everyone was hurting for fuel. In the end we just setup for an approach, called over the radio ‘British Officers coming through!’ and landed, much to the annoyance of the Italian air traffic controllers. The general consensus amongst the four Tornado crews I was with was, better to save the four jets and lose the one.
Eventually the broken jet arrived, the junior pilot suitably embarrassed about not asking the fuel situation of the four lead jets prior to declaring an emergency that air traffic could do absolutely nothing about.
We carry check cards which have fuel figures at intervals of 100 kgs, 10 minutes or 50 nautical miles depending on what you are trying to calculate but it’s often easier to just do it mentally as the cards require interpolation which is never fun.
‘Interpolation – In the mathematical field of numerical analysis, interpolation is a method of constructing new data points within the range of a discrete set of known data points. Pilots cannot be bothered with this and would rather do complicated mental arithmetic because they are heroes.’ – Definition mixed with author’s interpretation.

When I first started out in flying training I would wish to be able to take a calculator flying with me – even one of those old Casio calculator watches would have done.
With hindsight, I now know that it would have taken up so much more of my time, it was so much easier to learn some tricks and tips about how to do quick and robust maths.
There are times to do maths and there are times not to – I expect you’ve all been hunting for a parking spot in busy traffic when you’ve reached over and turned the radio off. This is because you are being sapped of mental capacity by having to listen to inane chatter on some talk show when you needed all of your faculties to concentrate on driving. It’s the same in the air – we call it ‘freeing up capacity’.
The mantra we use is ‘Aviate, Navigate, Communicate’ and all decisions are prioritised in that order precisely because this is the order that things will kill you the most quickly.
Let me explain…
If I lose control of the aircraft then I will crash so no matter if I am confused about where I am or I have an incoming radio call, I will always prioritise flying the aircraft over that. In fact, if a student of mine become ‘capacity saturated’ because of a difficult instrument approach, difficulty flying in formation at low level or responding to air traffic radio calls for example, an instructors response will always be the same ‘FLY THE AIRPLANE!’
What this means is that nothing is as important as keeping the aircraft in the air and, to respond to air traffic or check your map when ‘maxed out’ or extremely busy, is not the right thing to do. An incident back in 2015 highlights what happens when a pilot becomes task saturated and fails to prioritise the flying.
On 31 July 2015, a Saudi-registered Phenom 300 business jet crashed at Blackbushe Airport in the UK killing all onboard.
The pilot continued an unsafe and rushed approach, landing too far down the runway and at a higher approach speed than normal. The aircraft over-ran the end of the runway before bursting into flames and killing all onboard.
Investigators found that the pilot’s ‘mental capacity could have become saturated’ after being exposed to 66 audio warnings, instructions and messages during the three minutes and 32 seconds before reaching the start of the runway.
The report found that the pilot’s ability to adapt and take on new information as he was landing was impeded due to a ‘very high workload situation’.
It stated: ‘It is possible that in these circumstances the pilot … fixated on his initial strategy – landing – and lacked the mental capacity to recognise that the approach had become unstable and should be discontinued.’
The pilot, Mazen Salim Alqasim, 57, had 11,000 hours of flying experience and was conducting single pilot operations for which the Phenom 300 is certified.
When we instruct students we tell them that if it looks wrong, then it probably is. For the pilot of the Phenom 300 who had got himself task saturated, there was nobody to tell him that it looked wrong.
He had failed to prioritise.
So, before I attempt any maths or complicated planning airborne, I make sure that I have ‘free capacity’ to do the task. If I am mid-way through an activity when something happens to disturb me, I do one of two things.
1. Ignore it and carry on my task.
2. Park my task (maybe write on my kneeboard where I have got to so far) and complete the new task.
I don’t try and do both. Ever. (Secret: ‘This is how pilots die.’)
I’ve said before, pilots do not multi-task, they just do many tasks exceptionally quickly. They compartmentalise, parking some tasks whilst attending to other more important ones.
I liken it to trying to make your mind resemble a blank piece of paper. Every time a request for your attention comes in, it takes up part of that piece of paper and your job is to remove it from the paper as fast as you can so that there is space for another task to come in. When the paper becomes full, you’d better be careful as this is the part where pilots fly into the ground.
So, maths in the air. It all comes down to, what I call ‘Approximate and Refine’. The reason we do this is that, in a lot of cases, an approximate answer is just good enough and this is because our environment is rapidly changing and, well, maths in the cockpit is just really hard as a lot of other things are also happening!
If I take 30 seconds to calculate how long it will take me to cover 10 miles at 300 knots (or 5 miles per minute), then I have already covered 2.5 miles before I even have my answer so I need to approximate my answer first.
In fast jets we tend to work in ‘miles per minute’ (nautical miles to be exact but very similar to statute miles).
So using ‘approximate and refine’ – if I had to calculate 17 x 18 then I’d either say ‘it’s almost 20 x 20 so a little less than 400′ or a better refinement would be ‘15 x 20’ as 17 is closer to 15 and 18 is closer to 20. This now becomes much easier as we are multiplying by a factor of 10 and pilots who are busy just love adding a zero.
17 x 18 is similar to 15 x 20
17 x 18 = 306
15 x 20 = 300
…so it’s pretty similar, enough for Government work anyway!
Another quick way is to multiply 17 x 20 and then subtract (2 x 17 = 34) ie. 340–34 = 306
So there’s lots of ways to do it, just make it ‘approximate’ and then, if you have time and you are not too busy, ‘refine’.
Even 8 x 7 can sometimes be a really hard sum when you are super busy!
…maybe just do 10 x 7 and then subtract 2 x 7 (70–14) = 56
KEEP IT SIMPLE!
With fuel calculations we can approximate also – the Hawk at low level uses about 22.7 kgs per minute (at 7 miles per minute or 420 kts). So, wouldn’t it be better to just use 25 kgs per minute – that way we’ll always be safe as we would calculate a higher fuel burn than we were actually using?
So, over 5 minutes…
22.7 kgs per minute = 113.5 kgs
25 kgs per minute = 125 kgs
If I used the higher figure I would predict a higher fuel usage than I actually had so would be safer (25 is easy to calculate, 22.7 is not). As we then set off on our 5 minutes of flying, I could now refine my calcs and the best way of doing this is to often look at what is left over.
25 – 22.7 = 2.3
2.3 is about 10% of 25 so if we were to reduce our ’25 kgs figure’ by 10%, we’d get a more accurate fuel burn figure – this is ‘refining‘ but is only done if we have time and capacity to do it.
25 kgs per minute was 125 kgs, now reduce by 10% or 12.5 kgs and we get (125 – 12.5) = 112.5 kgs.
This is VERY close to the ‘22.7 kgs per minute figure’ of 113.5 kgs that we had above.
Practice percentage sums when you are in department stores – what exactly does 13% off actually mean?
If a fridge is ‘13% OFF’ then take its price, say £120, and ‘approximate and refine’
10% of 120 = 12
1% of 120 = 1.2
3 x 1% (3 x 1.2 = 3.6)
12 + 3.6 = 15.6
120 – 15.6 = £104.4
It gets easier the more you do it – never try and work out 9% of something when you can work out 10% and subtract 1%.
Speed distance time is something we use a lot – If you wish to practise this you can do it as you drive though it might be worth turning the ‘Archers’ off, especially if you are new to mental arithmetic.
If you are travelling in your car at 60 miles per hour, because there are also 60 minutes in an hour, you are covering 1 mile every minute – just take some time and think about that.
If you are driving at 120 mph, you are covering 2 miles every minute – this helps because if you have 7 miles to go, for example, and you know what you are covering every minute then the maths is simple.
20 miles at 2 miles EVERY MINUTE (120 mph) is 10 minutes, at 60 mph it would be 20 minutes.
Fast jets work in miles per minute for this reason. At low level, the Hawk flies at 420 kts or (420/60) 7 nautical miles per minute (knots) – this then makes the maths simpler.
‘OK, student pilot in the front seat, how long until we get home?’
‘Home is 35 miles away, we are flying at 7 nautical miles per minute so (35/7) = 5 minutes!’
So, more complicated – what about in our car at 80 miles per hour then?
Work out what 80 is in miles per minute (80/60) = 1.333 miles per minute which is going to be really hard to work with, so let’s just leave it as 8/6 then or, as a simpler fraction (divide everything by 2) which is 4/3.
Soooo…
Our speed is 4/3 ‘miles per minute’. If we know the distance we have to do, say 12 miles to the next service station, and our answer is in required in time, using the formula…

Rearrange to…

Or…

Which is also…
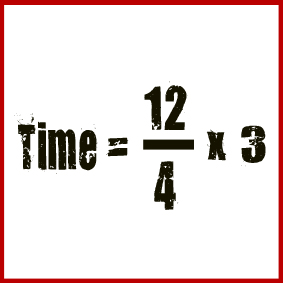
Which is 36/4 = 9 minutes
So, at 80 mph, you’ll cover 12 miles in 9 minutes.
Work with fractions when you can, brains don’t like multiple decimal places.
It also works for increasingly harder sums too!
If you have 80 miles per hour and 5 miles to go, just leave it all in fractions.
Distance over speed = 5/80 which is 5/80ths of an hour. So, multiply it all by 60 to get it into minutes… (it is actually the same as 1/16 but sometimes hard to see this, don’t worry!)
5/80 x 60 = 300/80 minutes
Get rid of the zeros… so now it’s 30/8, divide by the highest number you can,ie. 2. so 30/8 is now 15/4 minutes which is ALMOST 4 if we ‘approximate!’
So it’s 15/4 which is 3 and 3/4… what is 3/4 of a minute?
It’s 45 seconds…(60x 3/4 = 45 if you have to work it out, just re-multiply by 60)
The answer is 3 minutes and 45 seconds when we ‘refine‘.
Approximate and refine.
Hope that helps and, in all honesty, when it goes wrong – we just ignore everyone else and fly the jet, it’s saved my life a few times.
















